A Causal Continuous time Lti System is Described by the Equation

Latest Continuous Time LTI Systems MCQ Objective Questions

Continuous Time LTI Systems MCQ Question 1:

For the LTI system shown in the figure. Find impulse response of the system.

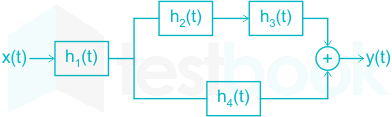
h₁(t) = h₂(t) = 5δ(t) ; h₃(t) = h₄(t) = u(t).

1. 20u(t)
2. 30u(t)
3. 10u(t)
4. 40u(t)

Answer (Detailed Solution Below)

Option 2 : 30u(t)

The correct answer is 30u(t)

Concept:

• When two blocks are in cascade form then take convolution of these two systems.
• When two blocks are in parallel to each other, then take the sum of these two systems.

Solution:

Here h₂(t) and h₃(t) are in cascade form.

\(\therefore\) h'(t) = h₂(t) * h₃(t)

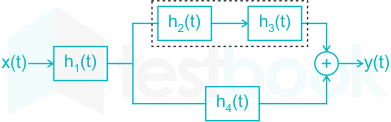
Now h'(t) and h₄(t) are in parallel.

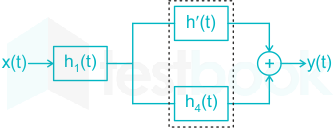
Therefore final system h(t) = h₁(t) * [ h'(t) + h₄(t)]

h'(t) =h 2 (t) * h 3 (t) = 5δ(t) * u(t) = 5u(t)

\(\therefore\) [h'(t) + h₄(t) ]= 5u(t) + u(t) = 6u(t)

\(\therefore\) h(t) =h 1 (t) * [ h'(t) + h 4 (t)]

 = 5δ(t) * 6u(t)

 = 30u(t)

Continuous Time LTI Systems MCQ Question 2:

Let an input x(t) = 2 sin(10πt) + 5 cos(15πt) + 7 sin(42πt) + 4 cos(45πt) is passed through an LTI system having an impulse response

\(\rm h(t) = 2 \left( \frac{\sin (10 \pi t)}{\pi t} \right) \cos (40 \pi t)\)

The output of the system is

1. 2 sin(10πt) + 5 cos(15 πt )
2. 5 cos(10πt) + 7 sin(15 πt )
3. 7 sin(42πt) + 4 cos(45 πt )
4. 2 sin(10πt) + 4 cos(45 πt )

Answer (Detailed Solution Below)

Option 3 : 7 sin(42πt) + 4 cos(45 πt )

Concept:

Fourier Transform of any time-domain function f(t) = \( {A sin ω_ct \over π t}\) is defined by:

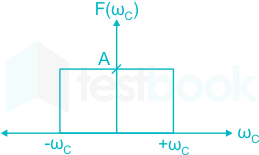
If f(t) is multiplied by any cosine term, then modified F(ω) is given by:

f(t) cos(ωt) = \( {f(w_c-w)+f(w_c+w)\over 2}\)

Calculation:

Given, f(t) = \( {2sin 10π t \over π t}\)

F(ω_c) is given as:

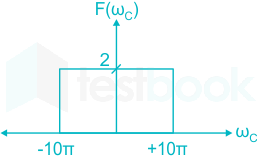
f(t) cos(40πt) = \( {f(w_c-40π )+f(w_c+40π )\over 2}\)

Applying shifting property in F(ω), we getf(ω_c - 40π) as:

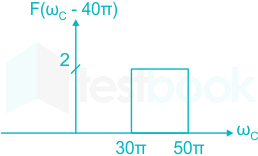      ---(i)

Applying shifting property in F(ω), we get f(ω c  + 40π) as:

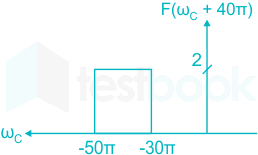      ---(ii)

Adding equations (i) and (ii) and dividing their sum by 2, we get:

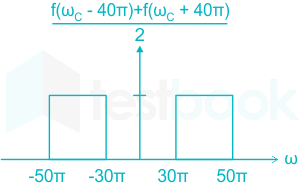
• input x(t) = 2 sin(10πt) + 5 cos(15 πt) + 7 sin(42πt) + 4 cos(45πt) has four different frequencies 10π , 15π , 42π and 50π .
• Frequency 10π and 15π lie outside the frequency band of above shown Fourier transform and will not pass, only frequency components 42π and 50π will pass.

Therefore, output y(t) =7 sin(42πt) + 4 cos(45 πt )

Continuous Time LTI Systems MCQ Question 3:

Let a causal LTI system be governed by the following differential equation

\(\rm y(t) + \frac{1}{4} \frac{dy}{dt} = 2x(t)\) where x(𝑡) and y(𝑡) are the input and output respectively.

Its impulse response is

1. \(\rm 2e^\left( - \frac{1}{4} t \right) u(t)\)
2. \(\rm 2e^{-4t} u(t)\)
3. \(\rm 8e^ {- \frac{1}{4} t} u(t)\)
4. \(\rm 8e^{-4t} u(t)\)

Answer (Detailed Solution Below)

Option 4 : \(\rm 8e^{-4t} u(t)\)

Concept:

The transfer function for a control system is defined as:

H(s) = \( {Y(s) \over X(s)}\)

where H(s) = Transfer function

Y(s) = Output function

X(s) = Input function

The impulse response for a control system is also known as the transfer function of the system.

Explanation:

\(\rm y(t) + \frac{1}{4} \frac{dy}{dt} = 2x(t)\)

Taking Laplace Transform on both sides:

∵ \(dy\over dt\)= sY(s)

\(\therefore \rm Y(s) + \frac{1}{4} sY(s) = 2X(s)\)

Y(s) \((1+{s\over 4})\)   = 2X(s)

Y(s) = 2X(s)

\({Y(s)\over X(s)}\)  = \({8\over s+4}\)

Taking Inverse Laplace Transform on both sides:

\({ 1\over s+a} \)= e^-at u(t)

\({y(t)\over x(t)}\)= 8e^-4t u(t)

Continuous Time LTI Systems MCQ Question 4:

Consider the following relation between input x[n] and output y[n] of a discrete system:

\(\rm y[n] = \sum_{k = 0}^{n^2} \cos \left( \frac{\pi}{4} k \right) x[k]\)

The system is

1. linear, time-invariant, causal and unstable
2. non-linear, time-variant, non-causal and stable
3. linear, time-variant, non-causal and stable
4. linear, time-variant, non-causal and unstable

Answer (Detailed Solution Below)

Option 3 : linear, time-variant, non-causal and stable

• Linear in x[n]
• Upper limit of summation operator is a function of n ⇒ Time variant
• n² > n ⇒ non causal
• When x[n] is bounded, y[n] is also bounded = Stable

Continuous Time LTI Systems MCQ Question 5:

Which of the following statements concerning the LTI system is correct?

1. If the impulse response of an LTI system is periodic and non-zero, then the system is unstable.

2. the inverse of a causal LTI system is always causal.

3. the cascade connection of a non-causal LTI system with a causal one necessarily produces a non-causal system.

1. 1 only
2. 1 and 2 only
3. 2 and 3 only
4. 1 and 3 only

Answer (Detailed Solution Below)

Option 1 : 1 only

Let us analyze each statement:

Statement 1:

For a system to be stable

\(\mathop \smallint \nolimits_{ - \infty }^{ + \infty } \left| {h\left( t \right)} \right|\;dt = finite\;value\)

If h(t) is periodic with period T (say), then:

\(\mathop \smallint \nolimits_{ - \infty }^{ + \infty } \left| {h\left( t \right)} \right|\;dt = N\mathop \smallint \nolimits_{ - \frac{T}{2}}^{\frac{T}{2}} \left| {h\left( t \right)} \right|\;dt\)

With N → ∞ denotes the number of cycles:

\(\mathop \smallint \nolimits_{ - \infty }^{ + \infty } \left| {h\left( t \right)} \right|\;dt \to \infty \)

Hence the system is unstable

Statement 1 is true.

Statement 2:

Let an LTI system which is causal is:

y(t) = x(t - t₀)

Its inverse system will be:

y(t) = x(t + t₀)

Which is non-causal

Hence statement 2 is false.

Statement 3 :

Let us consider a system as shown below:

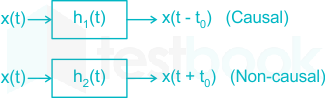
Cascade of two systems:

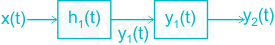
y₁(t) = x(t - t₀)

y₂(t) = y1(t + t₀)

y₂(t) = x(t - t₀ + t₀) = x(t)

So the cascade connection of a non-causal LIT system with a causal one producing causal system.

Hence, statement 3 is false.

Top Continuous Time LTI Systems MCQ Objective Questions

Consider a continuous-time system with input x(t) and output y(t) given by

y(t) = x(t)cos(t)

This system is

1. linear and time-invariant
2. non-linear and time-invariant
3. linear and time-varying
4. non – linear and time-varying

Answer (Detailed Solution Below)

Option 3 : linear and time-varying

Concept:

Linear system

The system is said to be linear if it follows Homogenous and Superposition property.

1) The system is homogenous if

y(t) = α₁x(t)

y(t) = α₂x(t)

2) The system follows Superposition if

y(t) = α1x(t) + α2x(t)

Time invariant system

if y(t - t₀) = x(t - t0)

and y(t') = x(t - t₀)

Analysis:

For the given signal check linearity property

y(t) = x(t)cos(t)

1) check homogeneity

y(t) = α1x(t)cos(t)

y(t) = α2x(t)cos(t)

2) check superposition

y(t) = α1x(t)cos(t) + α2x(t)cos(t)

The system follows both homogeneity and superposition thus the system is Linear.

check the time invariance

y(t - t0) = x(t - t0)cos(t - t0)

and y(t') = x(t - t0)cos(t)

since y(t - t0) ≠ y(t')

System is not time invariant.

Hence option (3) is correct

The continuous time system described by y(t) = x(t²) is

1. causal, linear and time varying
2. causal, non-linear and time varying
3. non causal, non-linear and time-invariant
4. non causal, linear and time-variant

Answer (Detailed Solution Below)

Option 4 : non causal, linear and time-variant

Concept:

Linearity: Necessary and sufficient condition to prove the linearity of the system is that the linear system follows the laws of superposition i.e. the response of the system is the sum of the responses obtained from each input considered separately.

y{ax1[n] + bx2[t]} = a y{x1[n]} + b y{x2[n]}

Conditions to check whether the system is linear or not.

• The output should be zero for zero input
• There should not be any non-linear operator present in the system

Causality: A system is causal, if the output of the system does not depend on future inputs, but only on past input.

Time-variance check:

y (t) =  x (t2)

Shifting the input first,

y (t,k) = x(t²- k)

Shifting the output,

y (t-k) = x((t-k)2)

y(t,k) ≠  y(t-k)

Given system is time variant.

Application:

The continuous-time system described by y(t) = x(t2)

The system depends on the future inputs and hence it is non-causal.

A time shift of t0 in the input does not give the t0 shift in the output and hence it is time-variant.

As there are no non-linear operators present, it is linear.

Therefore, the given system is non-causal, linear and time-variant

A continuous-time LTI system with system function H(ω) has the following pole-zero plot. For this system, which of the alternatives is TRUE?

1. |H(0 | > | ω |;| ω |>0
2. H(ω)| has multiple maxima, at ω₁ and ω₂
3. | H(0) | < |H(ω)| ; | ω | > 0
4. | H(ω) | = constant; -∞ < ω < ∞

Answer (Detailed Solution Below)

Option 4 : | H(ω) | = constant; -∞ < ω < ∞

Pole zero plot is redrawn as

As observed from the given pole-zero plot, poles & zeros are located symmetrically.

Therefore, it is all pass filter.

As we know that, from the property of all pass filter is,

• |H(jω)| = constant for all values of ω
• ∠H(jω) = Linearly vary with ω

Hence, the correct option is (4)

A continuous-time input signal x(t) is an eigenfunction of an LTI system, if the output is

1. k x(t), where k is an eigenvalue
2. Ke^iωt x(t), where k is an eigenvalue and e^iωt is a complex exponential signal
3. x(t) e^iωt, where e^iωt is a complex exponential signal
4. k H(ω), where k is an eigenvalue and H(ω) is a frequency response of the system

Answer (Detailed Solution Below)

Option 1 : k x(t), where k is an eigenvalue

A signal is said to be Eigen function if the output is scalar multiple of input signal and that scalar is referred as Eigen value.

Let input signal is x(t) and it is an Eigen function then

output = K x(t) where K is Eigen value.

A continuous, linear time-invariant filter has an impulse response h(t) described by

\(h\left( t \right) = \left\{ {\begin{array}{*{20}{c}} {3\;\;for\;0 \le t \le 3}\\ {0\;\;otherwise} \end{array}} \right.\)

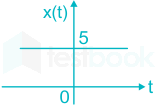
When a constant input of value 5 is applied to this filter, the steady-state output is_______.

Answer (Detailed Solution Below) 44 - 46

Concept :

A linear time-invariant system is given as:

y(t) = x(t) ⊕ h(t), i.e.

\(y\left( t \right) = \mathop \smallint \limits_{ - \infty }^\infty x\left( \tau \right)h\left( {t - \tau } \right)d\tau \)

Application :

Given x(t) = 5 (Constant) as shown:

Also, the impulse response of filter h(t) is given as:

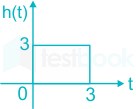
The output will be the convolution of the input and the impulse response, i.e.

\(y\left( t \right) = \;\mathop \smallint \nolimits_0^3 3.\left( 5 \right).dT\)

y(t) = 45

∴ The steady-state value of output is 45

A continuous time LTI system is described by

\(\dfrac{d^2y(t)}{dt^2} + 4 \dfrac{dy(t)}{dt} + 3y(t) = 2 \dfrac{dx(t)}{dt} + 4x(t)\)

Assuming zero initial conditions, the response y(t) of the above system for the input x(t) = e^-2t u(t) is given by

1. (e^t - e^3t) u(t)
2. (e^- t - e^- 3t​) u(t)
3. (e- t + e-​3t​) u(t)
4. (et + e3t) u(t)

Answer (Detailed Solution Below)

Option 2 : (e^- t - e^- 3t​) u(t)

Concept:

The transfer function is defined as the ratio of the Laplace transform of the output to that of the input with the initial conditions zero.

\(\rm TF=\dfrac{L[output]}{L[input]}\)

The Laplace transform for the integrated and differential signals are shown below:

\(\dfrac{dx}{dt} \longleftrightarrow sX(s)\)

\(\dfrac{d^2x}{dt^2} \longleftrightarrow {s^2}X(s)\)

\(\int x dt = \dfrac{1}{s} X(s)\)

The Laplace transform of the basic exponential signal is:

\(e^{-at}u(t) \longleftrightarrow \dfrac{1}{s+a}; \; ROC = \sigma > Re{(-a)}\)

\(e^{at}u(t) \longleftrightarrow \dfrac{1}{s-a}; \; ROC = \sigma > Re{(a)}\)

Calculation:

Converting the given time-domain differential equation into the frequency domain we get:

\(s^2Y(s)+4sY(s)+3Y(s)=2sX(s)+4X(s)\)

\(\frac{Y(s)}{X(s)}=\dfrac{2s+4}{s^2+4s+3}\)

\(Y(s)=\dfrac{2(s+2)}{(s+1)(s+3)}\frac{1}{s+2}\)

\(Y(s)=\dfrac{2}{(s+1)(s+3)}\)

\(H(s)=\dfrac{A}{s+1}+\dfrac{B}{s+3}\)

\(A=\left.\dfrac{2}{s+3}\right|_{s=-1}\)

\(A=\dfrac{2}{-1+3}=\dfrac{2}{2}=1\)

\(B=\left.\dfrac{2}{s+1}\right|_{s=-3}\)

\(B=\dfrac{2}{-3+1}=\dfrac{2}{-2}=-1\)

\(Y(s)=\dfrac{1}{s+1}+\dfrac{-1}{s+3}\)

\(y(t)=(e^{-t}-e^{-3t})u(t)\)

Let the input be u and the output is y of a system, and the other parameters are real constants. Identify which among the following systems is not a linear system:

1. \(\frac{d^3y}{dt^3}+a_1\frac{d^2y}{dt^2}+a_2\frac{dy}{dt}+a_3y = b_3u + b_2\frac{du}{dt}+ b_1\frac{d^2u}{dt^2} \) (with initial rest conditions)
2. \(y\left( t \right) = \mathop \smallint \limits_0^t {e^{\alpha \left( {t - \tau } \right)}}\beta u\left( \tau \right)d\tau \)
3. y = au + b, b ≠ 0
4. y = au

Answer (Detailed Solution Below)

Option 3 : y = au + b, b ≠ 0

Concept:

A system is said to be linear if it satisfies to properties:

Additivity:

If states that, if an input x₁(t) produces output y₁(t) and another input x₂(t) also acting along produces output y₂(t), then, when path inputs acting on the system simultaneously, produce output y₁(t) + y₂(t).

If x₁(t) → y₁(t)

x₂(t) → y₂(t)

then x₁(t) + x₂(t) → y₁(t) + y₂(t)

Homogeneity:

It states that if input is scaled by c, then output also scaled by same amount.

if x₁(t) → y₁(t)

then cx₁(t) → cy₁(t): c is any real or Imaginary number

Solution:

y = au + b

y(t) = au(t) + b

u(t) = u₁(t) + u₂(t)

y(t) = au₁(t) + au₂(t) + b

y(t) ≠ [au₁(t) + b] + [au­₂(t) + b]

y(t) ≠ y₁(t) + y₂(t)

Hence the system is non linear

y = au + b is a nonlinear system

For the linear time invariant systems that are Bounded Input Bounded stable, which one of the following statement is TRUE?

1. The impulse response will be integral, but may not be absolutely integrable
2. The unit impulse response will have finite support
3. The unit step response will be absolutely integrable
4. The unit step response will be bounded

Answer (Detailed Solution Below)

Option 4 : The unit step response will be bounded

Concept :

• BIBO (Bounded Input Bounded output stable system is a type of system in which for given bounded input output is bounded.
• On applying unit step input to the system then the response which we get is called unit step response.
• Condition for absolutely integrable.

\(\rm\displaystyle\int_{-\infty}^{\infty}|x(t)| dt < \infty\)

• Bounded signals are those whose value always remains less than a certain value & finite support implies that the duration of the signal is finite.

Explanation :

• Since the system is BIBO stable & the unit step function is bounded, the unit step response will also be bounded.

Note:

\(\rm\displaystyle\int_{-\infty}^{\infty}|u(t)| dt = \rm\displaystyle\int_{-\infty}^{\infty}1 dt = \infty\)

Therefore unit step response is NOT absolutely integrable.

Consider the following statements for a system given by

\(y(n) = x(n) \sum_{k = - \infty}^\infty \delta (n - 3k)\)

1. The system is linear.

2. The system is non-linear

3. The system is causal

4. The system is non-causal.

Which of the above statements is/are correct ?

1. 1 only
2. 2 only
3. 2 and 4 only
4. 1 and 3 only

Answer (Detailed Solution Below)

Option 4 : 1 and 3 only

Given system is:

\(y(n) = x(n) \sum_{k = - \infty}^\infty \delta (n - 3k)\)

Linearity:

For input x₁(n)

Output\(y_1 (n) = x_1(n) \sum_{k = - a}^\infty\delta (n - 3k)\)

For input x₂(n)

Output\(y_2 (n) = x_2(n) \sum_{k = - a}^\infty\delta (n - 3k)\)

and for input x₁(n) + x₂(n)

Output\(y_3 (n) = [x_1(n) + x_2(n)] \sum_{k = - a}^\infty\delta (n - 3k)\)

Since, y₃(n) = y₁(n) + y₂(n)

Hence the system is linear

Causality:

The output y(n) does not depend on future values of input, and hence the system is causal.

∴ System is linear and causal.

Note:Please note that the Question is asking as to whether the system is stable or not. If the Question was asking for a particular signal, then we would have concluded with the logic that you are mentioning, i.e. a signal f(x) is causal if it is zero for x < 0. But it is asking for the system y(n).

The response h(t) of a linear time invariant system to an impulse δ(t), under initially relaxed condition is h(t) = e^-t + e^-2t. The response of this system for a unit step input u(t) is

1. u(t) + e^-t + e^-2t
2. (e^-t + e^-2t) u(t)
3. (1.5 – e^-t – 0.5 e^-2t) u(t)
4. e^-tδ(t) + e^-2t u(t)

Answer (Detailed Solution Below)

Option 3 : (1.5 – e^-t – 0.5 e^-2t) u(t)

Concept:

The impulse response of a system is the response of the system to an impulse function.

The response of the system to any signal x(t), is given by the convolution of the input signal with the impulse response, i.e.

y(t) = x(t) ⊗ h(t)

Also, the multiplication is s-domain property states that:

\(y\left( t \right)\mathop \leftrightarrow \limits^{\;\;\;L.T.\;\;\;} \;X\left( s \right) \cdot H\left( s \right)\)

X(s) = Laplace Transform of x(t)

H(s) = Laplace Transform of h(t)

The above property is used to evaluate the response of a signal.

Application:

Given, x(t) = e^-t + e^-2t

x(t) = u(t)

y(t) = x(t) ⊗ u(t)

Taking the Laplace Transform, we get:

Y(s) = X(s) ⋅ H(s)

Given,

H(s) = L [e^-t + e^-2t]

\(H\left( s \right) = \frac{1}{{s + 1}} + \frac{1}{{s + 2}}\)

x(t) = u(t)

\(X\left( s \right) = \frac{1}{s}\)

So, Y(s) = X(s) ⋅ H(s)

\(Y\left( s \right) = \left( {\frac{1}{{s + 1}} + \frac{1}{{s + 2}}} \right)\frac{1}{s}\)

\(= \frac{{s + 2 + s + 1}}{{\left( {s + 1} \right)\left( {s + 2} \right)\left( s \right)}}\)

\(= \frac{{2s + 3}}{{s\left( {s + 1} \right)\left( {s + 2} \right)}}\)

y(t) is obtained by taking the inverse Laplace transform of the above.

We can partial fraction to simplify the above:

\(\frac{{2s + 3}}{{s\left( {s + 1} \right)\left( {s + 2} \right)}} = \frac{A}{s} + \frac{B}{{s + 1}} + \frac{C}{{s + 2}}\)

This can be written as:

⇒ 2s + 3 = A (s + 1) (s + 2) + B(s) (s + 2) + C(s) (s + 1)

For s = -1

⇒ 1 = B (-1) (1) + 0

⇒ B = -1        ---(1)

For s = 0

3 = A(2) (1) + 0

\(A = \frac{3}{2}\)       ---(2)

For s = -2

⇒ 2(-2) + 3 = C (-2) (-2 + 1) + 0

⇒ -1 = 2C

\(C = - \frac{1}{2}\)

\(Y\left( s \right) = \frac{3}{2} \times \frac{1}{s} - \frac{1}{{s + 1}} - \frac{1}{2} \cdot \frac{1}{{\left( {s + 2} \right)}}\)

Taking the inverse Laplace transform we get:

\(y\left( t \right) = \frac{3}{2}\;u\left( t \right) - {e^{ - t}}u\left( t \right) - \frac{1}{2}\;{e^{ - 2t}}u\left( t \right)\)

= (1.5 – e^-t – 0.5 e^-2t) u(t)

The output of a continuous-time, linear time-invariant system is denoted by\(T\left\{ {x\left( t \right)} \right\}\) where\(x\left( t \right)\) is the input signal. A signal\(z\left( t \right)\) is called eigen-signal of the system  , when\(T\left\{ {z\left( t \right)} \right\} = \gamma z\left( t \right)\), where \(\gamma \) is a complex number, in general, and is called an eigenvalue of\(T\). Suppose the impulse response of the system\(T\) is real and even. Which of the following statements is TRUE?

1. is an eigen-signal but  is not
2. ​\(cos\left( t \right)\;and\;sin\left( t \right)\)are both eigen-signals but with different eigenvalues
3. \(sin\left( t \right)\)is an eigen-signal but\(cos\left( t \right)\) is not
4. \(cos\left( t \right)\)and\(sin\left( t \right)\) are both eigen-signals with identical eigenvalues

Answer (Detailed Solution Below)

Option 4 : \(cos\left( t \right)\)and\(sin\left( t \right)\) are both eigen-signals with identical eigenvalues

Concept:

A signal is said to be Eigen function if the output is scalar multiple of input signal and that scalar is referred as Eigen value.

Let input signal is x(t) and it is an Eigen function then

output = K x(t) where K is Eigen value.

Explanation:

The impulse response is real and even, hence \(H\left( {j\omega } \right)\)  will also be real and even.

Since \(H\left( {j\omega } \right)\)  is real and even,\(H\left( {j{\omega _0}} \right)\; = \;H\left( { - j{\omega _0}} \right)\)

Now \(cos\left( t \right)\)  is input i.e. \(\frac{{{e^{jt}} + {e^{ - jt}}}}{2}\)   is input

Output\(\frac{{H\left( {j1} \right){e^{jt}} + H\left( { - j1} \right){e^{ - jt}}}}{2} = H\left( {j1} \right)\left[ {\frac{{{e^{jt}} + {e^{ - jt}}}}{2}} \right] = H\left( {j1} \right){\rm{cos}}\left( t \right)\)

If \(sin\left( t \right)\)  is input i.e.\(\;\frac{{{e^{jt}} - {e^{ - jt}}}}{2j}\)  is input

Output will be\(\frac{{H\left( {j1} \right){e^{jt}} - H\left( { - j1} \right){e^{ - jt}}}}{2j} = H\left( {j1} \right)\left[ {\frac{{{e^{jt}} - {e^{ - jt}}}}{2j}} \right] = H\left( {j1} \right)\sin \left( t \right)\)

So \(sin\left( t \right)\)  and \(cos\left( t \right)\)  are eigen signals with same eigen values.

A system provides output y_i(t) when x_i(t) is applied. If the system is said to be LTI then which of the following properties must satisfy?

(i).If the input is x3 = ax1(t) + bx2(t), then output must be y3(t) = ay1(t) + by2(t)

(ii).If the input is x(t – T), then the output must be y (t – T)

(iii).If the input is x3 = ax1(t) + bx2(t), then output must be y3(t) = ay1(t) * by2(t)

(iv).If the input is x(t – T), then the output must be y(t + T)

1. (i), (ii) and (iv)
2. (i), (ii) and (iii)
3. (ii), (iii) and (iv)
4. (i) and (ii)

Answer (Detailed Solution Below)

Option 4 : (i) and (ii)

Analysis:

The defining properties of any LTI system are Linearity and Time-invariance.

• Linearity means that the relationship between the input and the output are the result of linear differential equations, that is, differential equations employing only linear operators.
• A linear system that maps an input x(t) to an output y(t) will map a scaled input ax(t) to an output ay(t) likewise scaled by the same factora. And the superposition principle applies to a linear system: if the system maps inputs x₁(t) and x₂(t) to outputs y₁(t) and y₂(t) respectively, then it will map x₃(t) = x₁(t) + x₂(t) to the output y₃(t) wherey₃(t) = y₁(t) + y₂(t).
• Time invariance means that whether we apply an input to the system now or T seconds from now, the output will be identical except for a time delay of T seconds.
• That is, if the output due to input x(t) is y(t), then the output due to input x(t - T) is y(t - T). Hence, the system is time invariant because the output does not depend on the particular time the input is applied.

The following equation describes a linear time-varying discrete time system

1. y(k + 2) + ky (k + 1) + y(k) = u(k)
2. y(k + 2) + ky² (k + 1) + y(k) = u(k)
3. y(k + 2) + 3y (k + 1) + 2y (k) = u(k)
4. y(k + 2) + y²(k + 1) + ky(k) = u(k)

Answer (Detailed Solution Below)

Option 1 : y(k + 2) + ky (k + 1) + y(k) = u(k)

Concept:

Linearity: Necessary and sufficient condition to prove the linearity of the system is that the linear system follows the laws of superposition i.e. the response of the system is the sum of the responses obtained from each input considered separately.

y{ax1[t] + bx2[t]} = a y{x1[t]} + b y{x2[t]}

Conditions to check whether the system is linear or not.

• The output should be zero for zero input
• There should not be any non-linear operator present in the system.

Time invariant:The system is time-invariant (T.I) if the input and output characteristics don't change with time.

The time-varying nature is caused due to internal components.

T.I (Shift invariant) & T.V (shift dependent system)

If x(t) → y(t) then

X(t – t0) → y(t – t0)

\(T.I\;y\left( t \right){\left. \right|_{x\left( {t - {t_0}} \right)}} = y\left( t \right){\left. \right|_{t = \left( {t - {t_0}} \right)}}\)

Analysis:

Option 2 and 4 have non-linear operators hence they are not linear.

Option 1 is the only linear and time-variant system.

Let an input x(t) = 2 sin(10πt) + 5 cos(15πt) + 7 sin(42πt) + 4 cos(45πt) is passed through an LTI system having an impulse response

\(\rm h(t) = 2 \left( \frac{\sin (10 \pi t)}{\pi t} \right) \cos (40 \pi t)\)

The output of the system is

1. 2 sin(10πt) + 5 cos(15 πt )
2. 5 cos(10πt) + 7 sin(15 πt )
3. 7 sin(42πt) + 4 cos(45 πt )
4. 2 sin(10πt) + 4 cos(45 πt )

Answer (Detailed Solution Below)

Option 3 : 7 sin(42πt) + 4 cos(45 πt )

Concept:

Fourier Transform of any time-domain function f(t) = \( {A sin ω_ct \over π t}\) is defined by:

If f(t) is multiplied by any cosine term, then modified F(ω) is given by:

f(t) cos(ωt) = \( {f(w_c-w)+f(w_c+w)\over 2}\)

Calculation:

Given, f(t) = \( {2sin 10π t \over π t}\)

F(ω_c) is given as:

f(t) cos(40πt) = \( {f(w_c-40π )+f(w_c+40π )\over 2}\)

Applying shifting property in F(ω), we getf(ω_c - 40π) as:

      ---(i)

Applying shifting property in F(ω), we get f(ω c  + 40π) as:

      ---(ii)

Adding equations (i) and (ii) and dividing their sum by 2, we get:

• input x(t) = 2 sin(10πt) + 5 cos(15 πt) + 7 sin(42πt) + 4 cos(45πt) has four different frequencies 10π , 15π , 42π and 50π .
• Frequency 10π and 15π lie outside the frequency band of above shown Fourier transform and will not pass, only frequency components 42π and 50π will pass.

Therefore, output y(t) =7 sin(42πt) + 4 cos(45 πt )

Direction: Question consists of two statements, one labelled as the 'Assertion (A)' and the other as 'Reason (R)'.

Examine these two statements carefully and select the answer to this question using the codes given below:

Assertion (A): The system described by y²(t) + 2y(t) = x²(t) + x(t) + c is a linear and static system.

Reason (R): The dynamic system is characterized by differential equation.

1. Both A and R are individually true and R is the correct explanation of A
2. Both A and R are individually true but R isnot the correct explanation of A
3. A is true but R is false
4. A is false but R is true

Answer (Detailed Solution Below)

Option 4 : A is false but R is true

CONCEPT:

LINEAR SYSTEM-

A linear system follows the laws of superposition. This system is a combination of two types of laws –

• Law of additivity
• Law of homogeneity

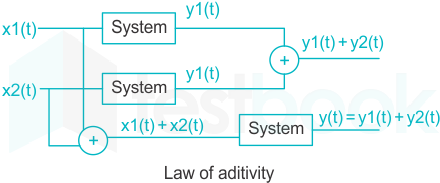
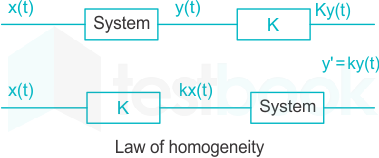
The conditions for a system to be linear are −

1. The output should be zero for zero input.

2. There should not be any non-linear operator present in the system.

Examples of non-linear operators −Trigonometric operators- Sin, Cos, Tan, Cot, Sec, Cosec, Exponential, logarithmic, modulus, square, Cube, Sa, Sinc, etc.

Either input x or output y should not have these non-linear operators.

STATIC AND DYNAMIC SYSTEM-

Static system is memory-less whereas dynamic system is a memory system.In memory less or static system the output is only dependent upon present input.Eg-1.y(t) = 4 x(t) is a static system, y(t) = 2 x(t) + 3 x(t-3) is a dynamic system.

The dynamic systems can be characterized by differential equations. Using differential equations we can easily get a solution for a dynamic system.

ANSWER-

ASSERTION EXPLANATION

The system equation has a square term of output y(t) as well as for input x(t) so this equation is non-linear. Statement (A) is incorrect.

REASON EXPLANATION-

Yes, we can characterize the Dynamic system by Differential equation so statement (R) is correct.

Let a causal LTI system be governed by the following differential equation

\(\rm y(t) + \frac{1}{4} \frac{dy}{dt} = 2x(t)\) where x(𝑡) and y(𝑡) are the input and output respectively.

Its impulse response is

1. \(\rm 2e^\left( - \frac{1}{4} t \right) u(t)\)
2. \(\rm 2e^{-4t} u(t)\)
3. \(\rm 8e^ {- \frac{1}{4} t} u(t)\)
4. \(\rm 8e^{-4t} u(t)\)

Answer (Detailed Solution Below)

Option 4 : \(\rm 8e^{-4t} u(t)\)

Concept:

The transfer function for a control system is defined as:

H(s) = \( {Y(s) \over X(s)}\)

where H(s) = Transfer function

Y(s) = Output function

X(s) = Input function

The impulse response for a control system is also known as the transfer function of the system.

Explanation:

\(\rm y(t) + \frac{1}{4} \frac{dy}{dt} = 2x(t)\)

Taking Laplace Transform on both sides:

∵ \(dy\over dt\)= sY(s)

\(\therefore \rm Y(s) + \frac{1}{4} sY(s) = 2X(s)\)

Y(s) \((1+{s\over 4})\)   = 2X(s)

Y(s) = 2X(s)

\({Y(s)\over X(s)}\)  = \({8\over s+4}\)

Taking Inverse Laplace Transform on both sides:

\({ 1\over s+a} \)= e^-at u(t)

\({y(t)\over x(t)}\)= 8e^-4t u(t)

If x(t) = e^-t u(t) and y(t) = e^-3tu(t), then y(t) * x(t) will be

1. (e^-t – e^-3t) u(t)
2. \(\frac{e^{-3t}-e^{-t}}{2}u(t)\)
3. \(\frac{e^{-t}-e^{-3t}}{2}u(t)\)
4. \(\frac{e^{-t}+e^{-3t}}{2}u(t)\)

Answer (Detailed Solution Below)

Option 3 : \(\frac{e^{-t}-e^{-3t}}{2}u(t)\)

Concept:

Some important convolution results are

• u(t) * u(t) = t u(t)
• e­-at u(t) * e­-at u(t) = t e­-at u(t)
• e­-t u(t) * u(t) = (1- e­-t) u(t)
• \({e^{ - at}} *{e^{ - bt}}= \frac{1}{{\left( {b - a} \right)}}{[e^{ - at}} - {e^{ - bt}]}\;u\left( t \right)\)
• \(t\;{\rm{u}}\left( {\rm{t}} \right){\rm{*u}}\left( {\rm{t}} \right) = \frac{{{{\rm{t}}^2}}}{2}{\rm{u}}\left( {\rm{t}} \right)\)

Calculation:

x(t) = e-t u(t) and y(t) = e-3tu(t)

Now convolution

h(t) =  x(t) * y(t)

\(h(t) = \frac{e^{-t}-e^{-3t}}{2}u(t)\)

What is the range of values of a and b for which the linear time-invariant system with impulse response \(h\left( n \right) = \left\{ {\begin{array}{*{20}{c}} {{a^n},}&{n \ge 0}\\ {{b^n},}&{n < 0} \end{array}} \right.\) is stable?

1. Both |a|<1 and |b|>1 are satisfied
2. Both |a|>1 and |b|<1 are satisfied
3. Both |a|>1 and |b|>1 are satisfied
4. Both |a|<1 and |b|<1 are satisfied

Answer (Detailed Solution Below)

Option 1 : Both |a|<1 and |b|>1 are satisfied

\(h\left( n \right) = \left\{ {\begin{array}{*{20}{c}} {{a^n},}&{n \ge 0}\\ {{b^n},}&{n < 0} \end{array}} \right.\)

For stability, h(n) must be absolute summable.

\(\mathop \sum \limits_{ - \infty }^\infty {\left| {h\left( n \right)} \right|^2} < \infty \)

\(\Rightarrow \mathop \sum \limits_{n = 0}^\infty {\left| {{a^n}} \right|^2} + \mathop \sum \limits_{ - \infty }^{ - 1} {\left| {{b^n}} \right|^2} < \infty \)

The above equation valid for |a|< 1 and |b|> 1.

wertzhopoick.blogspot.com

Source: https://testbook.com/objective-questions/mcq-on-continuous-time-lti-systems--5eea6a0839140f30f369d7fb

Share this post